Koester2007MaxBCGRedSequenceGalaxy
- maxBCG paper，是 redMaPPer 的更早版本
- 这里的 richness 在之后可以作为 cluster mass proxy
- companion paper Koester 2007: 用 maxBCG 从 SDSS 中发现了 13823 个 cluster，研究了算法的表现，还研究了光学 cluster 和 X-ray cluster 的关系
Comment #
- 光学相比 X-ray 在 cluster 研究上的优势
- 数据便宜、能够找到更暗的 cluster、有副产品产出
- 算法的基础：cluster 成员星系具有一定的特征
- 空间和颜色上聚集
- 在给定的红移上是最亮的星系
- 具有一个 BCG
- 具体的算法
- 首先是要对于每一个星系计算其作为 BCG 的概率
- 这里的概率要拆分成多个部分，分别研究
- 位置分布：NFW profile 的二维投影
- 颜色分布：周围的星系是否具有基本一致的颜色？
- BCG: 这个星系是否具有 BCG 独特的性质？
- 总的来说就是考察一个星系作为 BCG 的全方面的概率因素，整合到 likelihood 里面，然后对 likelihood 进行排序得到 cluster catalog
- cluster richness 由对周围满足一定条件的星系进行计数得到
- 其实这里相当于把 red sequence 当成了一个单一颜色的序列，也就是一个红移对应一个红的颜色，这样可以得到星系在视线方向上的距离信息
Abs #
- cluster 具有宇宙学的意义
- cluster 被识别为 an overdensity of bright, uniformly red galaxies
- BCG 在这种探测方法中也占据很重要的地位
- 研究了 BCG 在 mock galaxy catalog 上的表现
- 可以恢复出 halo abundance function, 以及得到 cluster richness 和 halo property 的关系
- 可能有时候会 over merge 视线方向上的其他结构，导致 red sequence galaxy 的数量被高估 <20%
1 Intro #
- cluster 是 DM halo 的观测对应，所以对于宇宙学具有重要的意义
- cluster 中暗物质含量超过 85%
- 普通物质中的大部分以 hot intracluster medium 形式存在
- 这种气体供给恒星的燃烧，还会发出 X-ray 以及产生 SZ effect
- 探测 cluster 的方法包括 X-ray, 光学和 SZ effect
- 研究宇宙学不仅需要 cluster finding, 更重要的是研究 observables 和 cluster mass 的关系，以及这个关系的 scatter
- 光学方法的优势在于高红移、高信噪比；但是会受到投影效应的影响
- X-ray 不会受到投影的影响，但是探测范围有限，只能看到高亮度/低红移的 cluster
- 光学数据是更便宜的
- 光学数据能够测量具有更低 abundance 的系统，也就是降低 abundance function 的下限
- 有利于加强宇宙学的限制
- 可以缓解 scatter
- 光学数据除了得到和宇宙学有关的 richness 之外还有额外的数据产出，比如星系 membership, 速度信息，光度函数等
- 通过光学数据得到 cluster catalog 是可能的，关键在于减少 projection effect
- red sequence 的方法最早提出于 Gladders&Yee 2000
- 之后还有两项推广的工作
- cluster finding algorithm 是重要的
- 算法最好能尽量简单、客观、自动化，并且可以提供 cluster 的其他物理信息
- 算法的基础是：cluster 中的星系倾向于表现出 early 形态以及比较红的颜色（这一段其实在下面 sec2 有更详细的描述）
- 红色星系的比例随着 halo mass/luminosity 的增长而升高，并且随着到 cluster 中心的距离增加而降低
- 也就是说，cluster 的演化倾向于将其中的星系变为红色和 early-type 的形态
- 红色星系的比例随着 halo mass/luminosity 的增长而升高，并且随着到 cluster 中心的距离增加而降低
- we present maxBCG, an optical cluster finding algorithm
- 原理：在特定红移下，cluster 成员一般是最亮的星系，并且在颜色和空间上具有聚集性质（clustered）
- 由以上性质可以选择出 richness 比较高的 cluster 并且确定其中心
- 对于 richness 较低的星系，则需要依靠已知的 red sequence 对 potential cluster 进行筛选
- volume-limited 意思是在给定体积内寻找某一亮度阈值以上的样本，和 flux-limited 相对
另一篇 paper 中给出了 maxBCG 在 SDSS 上的运行结果
2 Algorithm #
2.1 Outline #
cluster 具有三个主要特征
- 成员星系分布具有明显的 clustering, 在二维平面中以 1/r 的方式衰减
- 最明亮的星系在 CMD 中位于 red sequence (E/S0 ridgeline) 之上，具有非常一致的颜色，并且是给定红移下最亮、最红的星系
- 由于显著的 4000A break 特征，这些星系的颜色和红移是紧密关联的，可以从颜色推算红移
- 4000A break
- 主要是因为恒星的大气吸收以及没有温度达到 400nm 的高温恒星
- 另一种说法：line-blanketing
- 对应于比较冷的恒星
- Balmer break 出现在 3645A，对应 n=2 和自由态之间的跃迁
- 在 10000K 的 A star 中最明显
- 4000A break
- 由于显著的 4000A break 特征，这些星系的颜色和红移是紧密关联的，可以从颜色推算红移
- 一般具有唯一的中心最亮星系（BCG），和星系分布中心重合，可以用于确定 cluster 的存在、位置和红移
将以上的 feature 整合到一个 likelihood 里面，然后评判每一个星系是否可能是每个红移上的 BCG（需要一个 galaxy catalog 作为输入）
- 对于一个星系，寻找其 likelihood 最大的红移值
- 将星系的最大 likelihood 进行排序
- likelihood 最大的星系成为第一个 cluster center, 排除周围一定空间范围内的星系作为 BCG 的可能性
- 以上过程称为 percolation, 最后得到了一个 cluster catalog, 其中包含中心星系和红移信息
- 对周围星系作距离、颜色和光度的截断，将周围星系的数目作为 cluster 丰富度 $N_\mathrm{gal}$ 的估计值
- 另一个估计值是 $N_\mathrm{gal}^\mathrm{R200}$，采用可变的 aperture
2.2 Likelihood #
由两部分组成，$\mathcal{L}\mathrm{BCG}$ 衡量单个星系作为 BCG 的可能性，$\mathcal{L}\mathrm{R}$ 衡量周围环境和 red sequence 匹配的程度（R for ridgeline）
目的之一是为了找到最合适的红移
2.3 Ridgeline likelihood #
对应上面的 $\mathcal{L}_\mathrm{R}$
Ridgeline likelihood 分解为空间和颜色的 filter
Spatial filter #
cluster 周围的 DM halo 和星系的分布都可以用 NFW 来近似
$$
\rho(r) = \delta_{c} \rho_{c} \frac{1}{(r/r_{s})(1+r/r_{s})^{2}}
$$
其中 $r_s=R_\mathrm{200}/c$ 是 scale radius. 将这个分布投影到二维上得到
$$
\Sigma ( x ) = \frac { 2 \rho _ { s } r _ { s } } { x ^ { 2 } - 1 } f ( x )
$$
由这个 filter 对到中心不同距离的星系赋予不同的权重，这样可以增大真正满足这样分布的星系的 likelihood (有点类似图像处理里面卷积一个和 psf 同样大小的 kernel)
~~在 This work 中设置固定的 $r_s$ 为 150kpc~~
Color filter #
对于 cluster 的研究表明存在一个 universal 的 red sequence, 对于低红移和高红移的 cluster 都成立
- 这些 red sequence 星系是 cluster 中最亮的星系，主要由 E 和 S0 (透镜) 组成，这是 E/S0 ridgeline 名称的来源
- 形成这样的 sequence 的原因是星系基本由年老的恒星组成，也就是最近很长时间以来都没有 SF 活动
- 关于 red sequence 的 review 可以参考 G&Yee 2000 的文章
- cluster 之外（比如 group）也存在类似的 rs
- field spiral 星系可以过渡到 rs 星系，这一过程可以由以下步骤实现
- spiral 星系发生碰撞产生椭圆星系
- 椭圆星系由于 ram pressure 等原因失去 hot gas, 进而使得 SF 停止
- 以上 picture 得到了最近的 simulation 的补充，AGN feedback 对此也有贡献
- 可能在 group 中没有非常明显，但是 rs 这个概念仍然是存在的
- field spiral 星系可以过渡到 rs 星系，这一过程可以由以下步骤实现
This work 根据 SDSS g-r 和 r-i 进行颜色的 cut, 依赖于已知的 rs 给出的颜色-红移关系
- 首先根据 SDSS 的数据定义一个 red sequence (CMD 上的一条 line), 并且测量其 width
- 投影得到颜色的 marginal distribution, 基本满足 Gaussian 分布, scatter 大约是 0.05 水平
- line scatter (width) 基本是 intrinsic 的
- 这里似乎忽略了 rs 的 small tilt?（通过上面的 projection）也就是不考虑颜色相对于亮度的依赖关系？
- normalization function 具有 Gaussian 形式，将 being tested galaxy 的颜色和给定红移上的平均颜色进行对比
- Gaussian function 的方差来源于两个 error 的平方和：galaxy 本身的测量误差以及 rs 的 intrinsic error (0.05 level)
- 如果星系满足理论的红移-颜色关系的话，这个 Gaussian 会达到最大值，这是一个推测星系红移的方法
- 对于星系测量误差较低，或者 cluster red sequence 比较明显的情况，推测的红移会非常精确
- 好处是将星系的颜色 error 也纳入了考虑中，一些测光误差较大的星系提供比较有限的信息
- 不需要完美的 color-redshift 关系，但是一个准确的关系是有帮助的
- 4000A break 使得 g-r 成为一个对于 red sequence 星系来说有效的红移 indicator, 所以得到精确的红移是完全可能的
- 光度红移？
- 在 maxBCG 中，颜色-红移关系是通过已知颜色和红移的 SDSS LRG 作为模板来得到的（数据来源于 Eisenstein 2001）
- 原因是 LRG 样本中包含很多 cluster galaxy (因为 cluster galaxy 一般也是比较明亮、比较红的)
- 但是 LRG 的这种关系仅在 z>0.15 有效
- 可能因为 LRG 的选择在低红移下不那么 robust
- 对于 z<0.15 this work 使用了一些另外的方法筛选 SDSS 光谱星系
- 用颜色-红移关系来寻找 cluster galaxy, 然后用这些样本反过来校准颜色-红移关系
下面是一定红移范围内的颜色-红移关系及其 scatter（dot 应该是用作 template 的 LRG? 两条虚线分别对应纯粹 passive 星系和纯粹 star-forming 星系的颜色-红移关系，实线是拟合得到的 function?）
总之这一步的目的就是得到 Gaussian 分布中的 $x(z)$，忽略颜色对星系光度的依赖关系
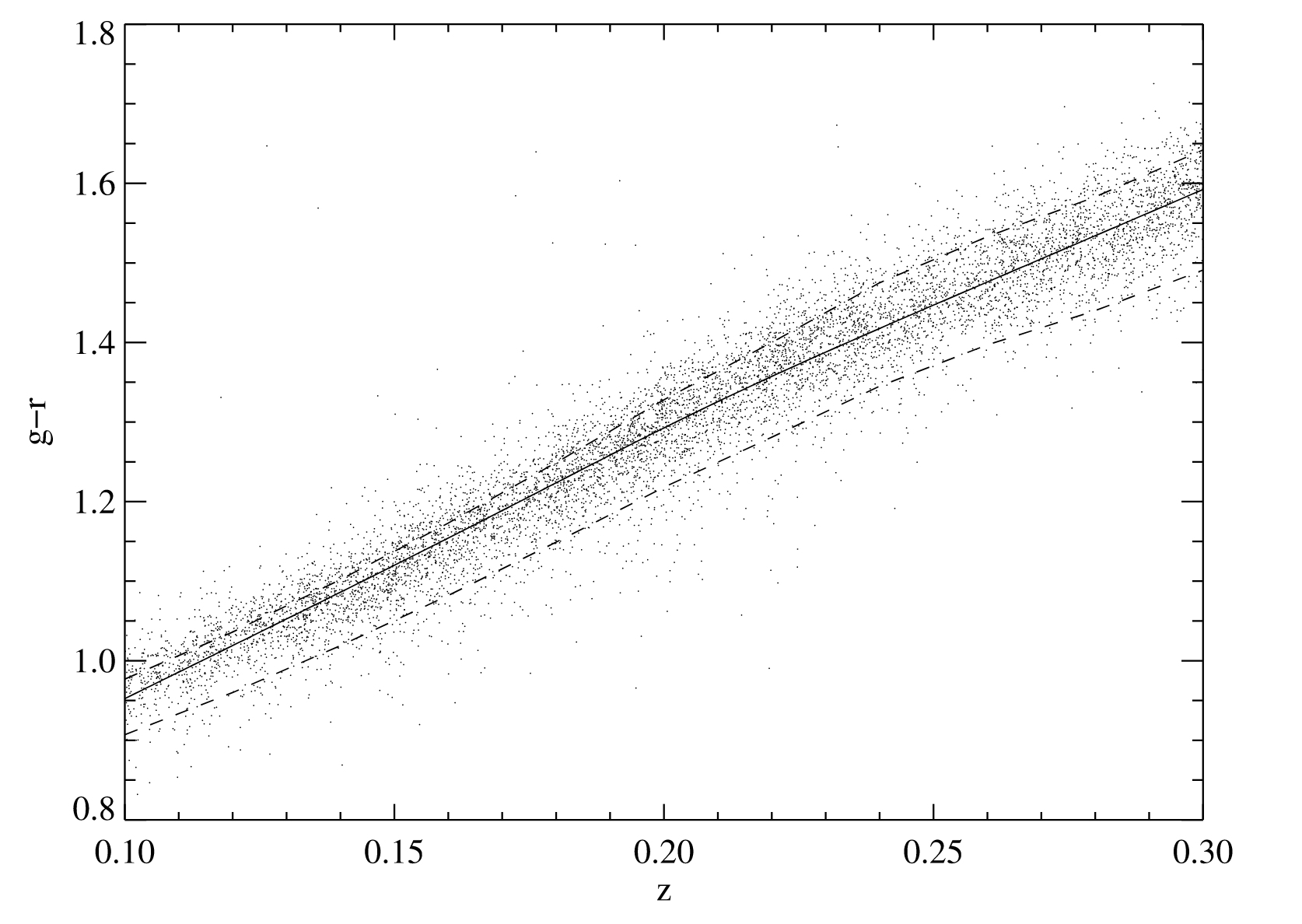
关于颜色-红移关系的确定有很多问题：
- 这里的实线是怎么拟合的？
- 似乎还有一个确定 cluster galaxy 之后再回去重新优化颜色-红移关系的步骤？
- 这里的点似乎是 cluster member, 而不是 LRG? 但是又是具有光谱数据的 member
Constructing $\mathcal{L}_\mathrm{R}$ #
这里的过程是 Postman et al. (1996) 的简单复述（可以去看 Postman 的 sec4）
$$
\mathcal{L}_R \sim \frac{1}{\sigma} \exp \left\{ \frac{\left[ b(c) + \Lambda_N M(r,c) - D(r,c) \right]^2}{\sigma^2} \right\}
$$
- $M(r,c)$ 是关于位置参数 $r$ 和颜色 $c$ 的分布模型，用作 filter 以匹配实际满足这个分布的 cluster center, 前面的 $\Lambda$ 是 cluster richness
- $M=\Sigma(r /r_\mathrm{s}) G_\mathrm{g-r}G_\mathrm{r-i}$
- 这里 $\Sigma$ 代表的是 NFW profile 投影到二维上的分布，后面是两个关于颜色的 Gaussian 分布
- 这里的 $r$ 说明是成员星系而不是 BCG?
- 将 Poisson 分布近似为 Gaussian
- $b(c)$ 是 background
- number count 被背景主导，所以 $\sigma^2\approx b(c)$
- 这里的 $D(r,c)$ 是某种形式的基准，或者说是某一个 Gaussian 的均值
- 以上 $M(r,c)$ 是理论的分布（model），而这里的 $D$ 可能来源于实际数据
- 是实际数据中每一个星系的 likelihood 计算？
对于一个给定的 cluster 中心，需要对周围区域进行积分
$$
\ln \mathcal{L}_R \propto \int \frac{\Sigma(r/r_s) G_{g-r} G_{r-i}}{b(c)} d^2 r \, dm \, dc
$$
（也许这里的数学推导可以跳过？因为确实用不到，只需要了解算法的步骤就可以；具体的算法需要去看 Postman 1996 的文章）
将似然函数应用到一个星系为中心、周围有很多 potential member galaxy 的模式中，上面的积分就转化为求和
$$
S(\theta) = \sum_{k=1}^{N_g} \Sigma(r_k(\theta)) G_{g-r}(c_k) G_{r-i}(c_k)
$$
（最后这个函数就是最直觉的形式~~，所以推导根本没用~~）
这里的问题：
- $D$ 是什么？是如何从实际数据中构造的？
- 什么时候加入了星等 m 这一个变量？
- 为什么是 Poisson?
- 应该是 $-\ln \sigma$？
总之就是结论很简单，但是过程没有清楚
最后这个 likelihood 综合考虑了一个星系周围邻居的位置分布以及颜色分布，如果位置分布类似
2.4 BCG likelihood #
BCG #
BCG for brightest cluster galaxy
likelihood 的第二个因子 $\mathcal{L}_\mathrm{BCG}$ 应当独立于周围环境进行计算
- cluster 一般都有一个 BCG
- 也称为 cD, central Dominant
- 其亮度变化服从 $r^{-1 /4}$ 的规律
- 亮度可以达到 10Lsun
- 属于 cluster 中一类独特的 galaxy population
- 位于 red sequence 的最亮端
- 可以利用 BCG 的独特性质寻找这类星系
- Koester 2007 的包含 99 个 cluster 的目录中 BCG 的性质如下
- 其中 79 个具有明确的 BCG
- 大部分颜色位于 red sequence 颜色范围的 0.1 以内
- BCG 大部分和 cluster X-ray 中心重合
- 需要一个 BCG catalog 以确定 BCG 的共同性质
- 在明亮的 LRG 样本中挑选出 BCG（人工手段）
- 进行颜色和红移空间的线性回归
- 用这些 LRG 作为模板搜寻 BCG, 然后构建更加精确的 BCG catalog
- 得到了 BCG 的亮度和红移的关系，用二次函数进行拟合
- 而 BCG 颜色随红移的变化关系可以直接参考 red sequence 的结果
最后的 likelihood 是
$$
\mathcal{L}_R(z) = G_{g-r}^{\mathrm{BCG}}(z) G_{r-i}^{\mathrm{BCG}}(z) \exp \left( -\frac{(m - m_i)^2}{\sigma_c} \right)
$$
后面的因子是星等组分，衡量星系有多大概率满足给定红移上 BCG 的亮度条件。
2.45 小结 #
likelihood 中的全部因子衡量的是下面几件事情：
（对于给定的一个星系和某个红移 z）
- 这个星系的颜色和亮度是否满足作为这个红移上的 BCG 的要求
- 周围星系是否满足位置的集聚性质
- 周围星系是否满足给定红移上的颜色条件
2.5 输入的星系目录 #
（这段唯一的信息就是确定 $L_\star$ 的细节）
- 首先把 catalog 根据红移分解为不同的 slice，然后进行基于颜色和星等的初步筛选
- input catalog 中星系的红移是已知的？
- 对星等的筛选标准为 $a(z)+M_\star$
- 其中 $a(z)$ 包括了全部 distance, k-correction, evolution 的影响
- 星等筛选可以满足 volume limited 的要求？
- 最后选择了 0.4 $L_\star$ 作为最小的光度值，记作 $L_\min$
- 还进行了 simulation 确定 k-correction 的影响
- 筛选 BCG 的时候，不会将比 tested galaxy 更亮的星系当作成员星系，因为 BCG 一般是最亮
3 Evaluating likelihood #
一些准则
- 作为 potential BCG, 一个星系必须位于 red sequence 颜色的 $3\sigma$ 误差之内，并且亮度超过 $L_\min$
- 这个限制将 tested galaxy 置于某段 $\pm0.05$ 的红移范围内
- 作为 neighbor galaxy, 必须在 BCG 周围 $3h^{-1}$ Mpc 以内
- neighbor galaxy 也需要满足以上的颜色和光度条件，并且比 BCG 更暗
- 以上的颜色误差 $\sigma$ 来源于星系测光的误差以及 red sequence 本征误差两方面
图 4 和图 5 展示了一个例子，由 likelihood 基本可以确定星系最可能的红移
具体的方法是
- 对于每个星系都可以进行这样的过程，得到每一个潜在 BCG 的最有可能的红移、周围 neighbor 的数量、最大的 likelihood 等信息
- 按照 likelihood 进行排列，将最大的定为 BCG，然后将红移和距离比较靠近的星系都标记为 cluster member
- 这个过程称为 percolation
- 被 flag 的星系不再作为可能的 BCG
- 抛弃少于 10 个星系的 cluster
- red sequence 不好定义
- 其中的 BCG 可能和大 cluster 的 BCG 性质略有不同
4 maxBCG selection function #
算法的测试：变量包括红移、richness
这里首先用了 Monte Carlo 方法：
- 将 SDSS 星系目录随机打乱、重新分配颜色、改变位置，用于模拟存在的干扰
- 然后加入真正的几个 Abell 星系团，位于不同的红移
理想情况是 maxBCG 将这几个 cluster 都找出来，并且可以给出正确的红移；但是这里测试集和训练集都来自 SDSS 不会有问题吗？
测试结果 #
完备性随着 galaxy number 升高而升高，普遍高于 90
更先进的方法：mock Galaxy catalog #
讲了一大堆为什么使用 mock 数据的原因
4.2 介绍了 richness 和 cluster mass 的关联